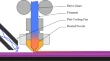
Tools, Methods, and Impact of Digitally Enabled Materials Engineering
Integrating Materials and Manufacturing Innovation is a journal committed to building a digital framework for materials and manufacturing design supporting the accelerated discovery, development, and application of materials and processes. The journal explores innovations that embrace the discipline of Integrated Computational Materials Engineering (ICME).